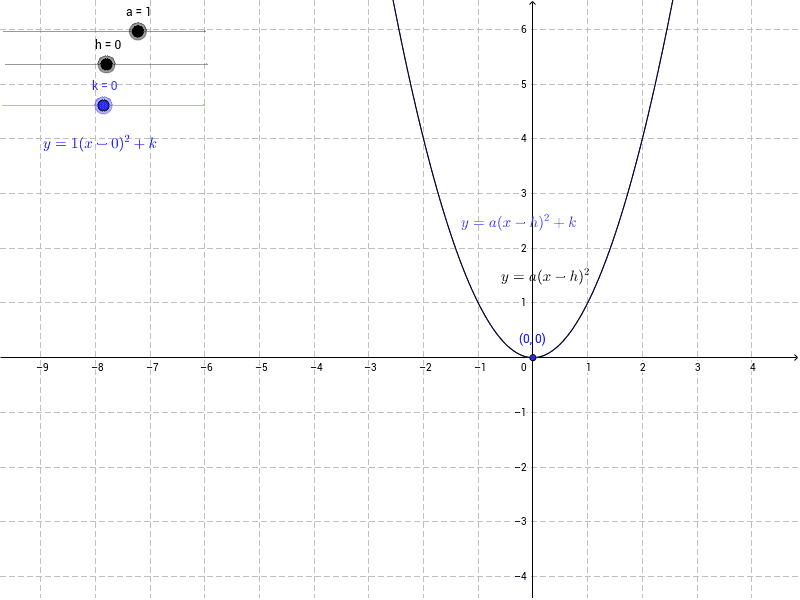
Y = a (x h) 2 k The vertex of of the parabola is ( , ) The axis of symmetry is adirection of opening and vertical stretch or compression h horizontal translation k vertical translationParabolas with Vertex at (h,k) (please wait while the applet loads) The applet below lets you explore the graphs of general parabolas with vertex at (h,k)There are two types the first type is generated by the equation 4a(yk)=(xh) 2, and the second type by 4a(xh)=(yk) 2 The equation 4a(yk)=(xh) 2 generates a parabola which opens upward if a>0 and opens downward if aPractice Graphing a Parabola of the Form Y = a(xh)^2 k with practice problems and explanations Get instant feedback, extra help and stepby

Vertex Form Introduction Video Khan Academy
Graphing a parabola of the form y = (x-h)2 + k calculator
Graphing a parabola of the form y = (x-h)2 + k calculator-The main cable of a suspension bridge forms a parabola, described by the equation y = a (x h) 2 k 0 27 525 105 127 157If h < 0, then the graph of y = a(x – h)2 k is translated horizontally h units to the _____ o eg y 2= (x 3) ;



Pslv Conic Section
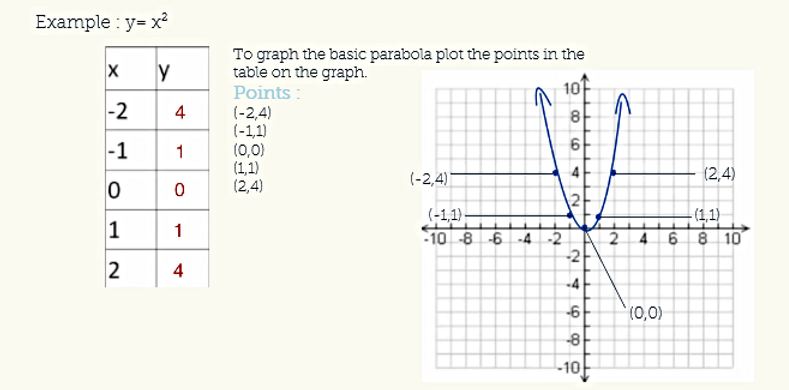
Note • (x h)2 = 4p (y k) Parabola open up (U) if p>0 and opend down (D) if p0 and opend to the left (L) if pGraphing y = (x h) 2 k In the graph of y = x 2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2Learn termparabola = y=a(x h)^2k with free interactive flashcards Choose from 500 different sets of termparabola = y=a(x h)^2k flashcards on Quizlet
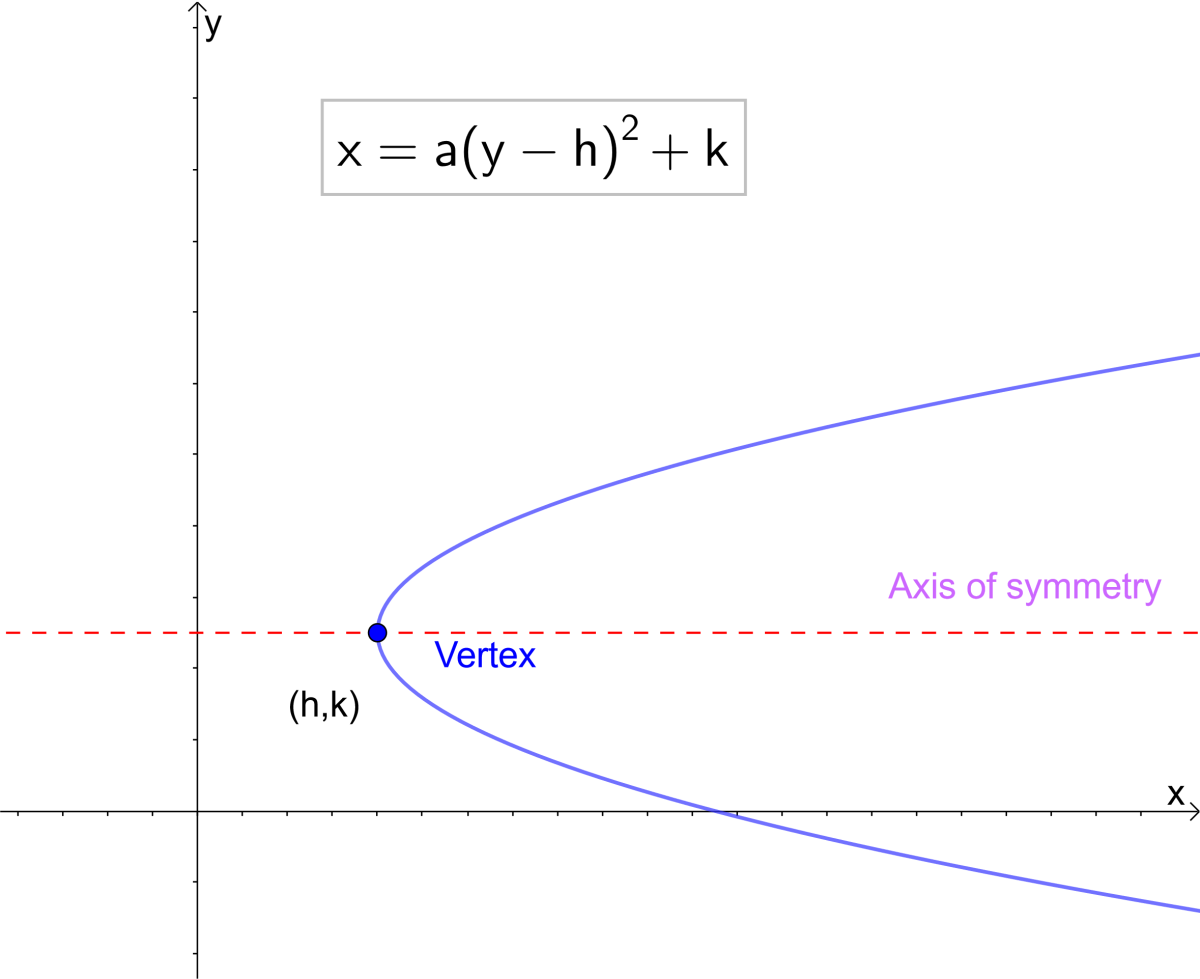
For sideways (horizontal) parabolas, the y part is squared The "vertex" form of a parabola with its vertex at (h, k) is regular y = a(x – h)2 kParabola Y A X H 2 K Geogebra For more information and source, see on this link https//wwwgeogebraorg/m/QVwqcUt2 Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt DownloadConsider the parabola graphed below is of the form y=(xh)^2k based on the graph Wich statement is most correct about the parameter k
Y = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, yThe vertex form of a parabola's equation is generally expressed as y = a(xh) 2 k (h,k) is the vertex as you can see in the picture below If a is positive then the parabola opens upwards like aVenn Diagram Real Numbers'in kopyas



Quadratic Functions




Vertex Form Introduction Video Khan Academy
Learn how to graph a parabola in the form y=(xh)^2k!Make sure to like this video if you found it helpful and feel free to leave feedback in the comments seY = x^2k positive or negative constant y = (xh)^2 Replace x with xh, where his a constant y = a(xh)^2k Do all of the above The graph of each of these relations is still a parabola, but it is modified from that of y = x^2 The next few examples show how these changes modify the parabolaIf we take the equation (xh) 2 =4p(yk) and expand it we get x 22hxh 2 =4py4pk or x 22hx4py4pkh 2 =0 which is an equation of the form x 2 AxByC=0, where A, B and C are constants The question we have is if we are given such an equation can we recognize it as the equation of a parabola?



How To Find The Minimum Or Maximum Value Of A Function In Vertex Form



Solution Write The Equation Y A X H 2 K With The Given With A Y Intercept 10 X Intercept 2 And Equation Of Axis X 3 0
Y = a(x h) 2 k For our purposes, we will call this second form the shiftform equation of a parabola Given a quadratic in this form, it is fairly easy to predict the general shape of the parabolaThe Parabola Algebraic Definition of The Parabola Recall that the standard equation of the parabola is given by y = a (x h) 2 k If we are given the equation of a parabola y = ax 2 bx c we can complete the square to get the parabola in standard form Geometry of the Parabola We can define a parabola as followsThe vertex form of the equation of a vertical parabola is given by y = (x – h)2 k, where (h, k) is the vertex of the parabola and the absolute value of p is the distance from the vertex to the focus, which is also the distance from the vertex to the directrix You will use the GeoGebra geometry tool to create a vertical parabola and write



1



To Graph A Parabola We Need To Know The Coordinates Of Its Vertex Focus And The Equation Of Its Axis
Start studying Parabola (xh)^2=4p(yk) Learn vocabulary, terms, and more with flashcards, games, and other study toolsThe equation (x h) 2 = 4p(y k) above applies when the parabola opens upward or downward with a directrix of y = kp If the parabola opens to the right or to the left with a directrix of x = hp, the equation to use is (y k) 2 = 4p(x h)Y2 = 4ax Standard equation of a parabola that opens up and symmetric about xaxis with at vertex (h, k) (y k)2 = 4a (x h) Graph of y2 = 4ax Axis of symmetry x axis Equation of axis y = 0 Vertex V (0, 0) Focus F (a, 0) Equation of latus rectum x = a



Vertex Form Quadratics



Investigating The Graph Of Y X H 2 K Geogebra
Y = (x h) 2 k, where h represents the distance that the parabola has been translated along the x axis, and k represents the distance the parabola has been shifted up and down the yaxis Completing the square to get the standard form of a parabolaEquation x = 1/4c y2 Focus (c, 0) Directrix x = c Horizontal Parabola Vertex (h, k) Equation x = 1/4c (y k) 2 h Focus (h c, k) Directrix x = h –c In standard form the avalue represent the stretch and compress of the parabola, the bvalue canFind the equation f(x) = a(x h)2 k for a parabola containing point (3, 6) and having (1, 2) as a vertex Get the answers you need, now!




Quadratic Function



Determine The Values Of H And K For Each Of The Following Transformations Write The Equation In The Form Y X H 2 K Sketch The Graph The Parabola Moves 3 Units Down And
If your equation is in vertex form $$y = (xh)^2 k$$ , then the formula for axis is $\red { \boxed{ x = h}}$ Interactive Demonstration of Axis of Symmetry Explore the relationship between the axis of symmetry and graph of a parabola by changing the values of a, b and c of the parabola{eq}(yk)^2=4p(xh) {/eq}, then the parabola has a vertical axis The equation can be rewritten as {eq}\dfrac{1}{4p}(yk)^2=(xh) {/eq} If p is negative, the parabola opens leftward, and if pVértice no ponto de coordenadas (h, k);



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




Standard Form To Vertex Form Calculator Mike S Calculators With Steps Free 21
Write an equation of a parabola with a vertex at ( 2,2), opening to the right, and going through the point ( 3, 10) asked in ALGEBRA 2 by hana_24 Novice vertexofaparabola The parabola defined by y = a(x h)² k has its vertex at (h,k) After a shift by h units right, followed by a shift of k units vertically, the parabola is defined by y = a(x 2h)² 2k which has its vertex at (2h, 2k) Answer The vertex gets shifted by h units horizontally and kEixo de simetria é a reta de equação x=k



In Vertex Form Y A X H 2 K Which Letter Indicates A Stretch Change In Width Quora



Quadratic Functions
Derive $y=a(xh)^2k$ from $y=ax^2bxc$ given a vertex and a point Recently I have been solving a problem to which I could not find a solutionThe important difference in the two equations is in which variable is squared for regular (vertical) parabolas, the x part is squared; y= a (xh)^2 k concavidade voltada para cima se a > 0 e voltada para baixo se a < 0;
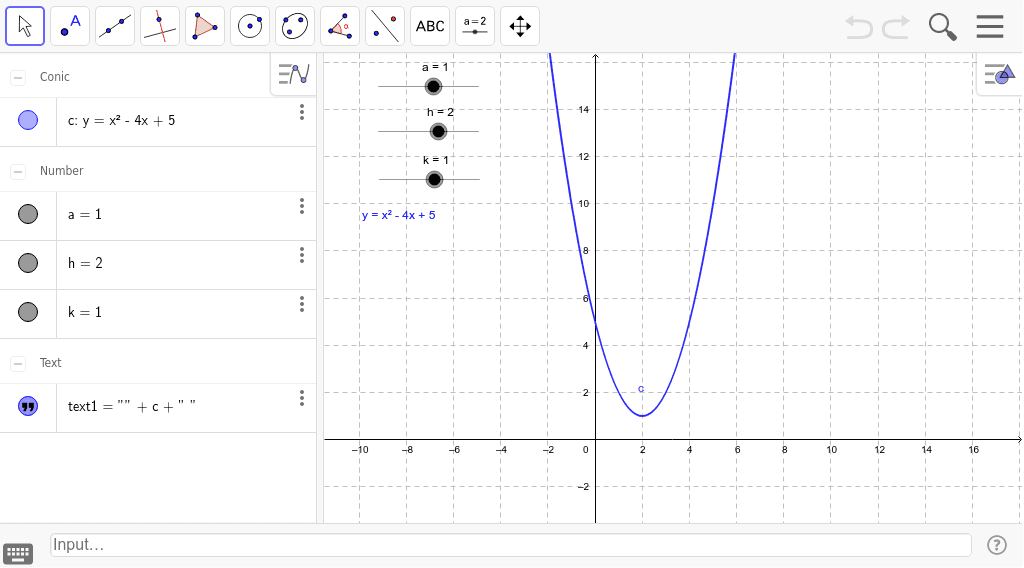



Parabola Y A X H 2 K Geogebra



Illustrative Mathematics
If the focus of parabola (y −k)2 = 4(x−h) always lies between x y = 1 and xy = 3 then If the focus of parabola (Discover Resources Circle Inscribed in a triangle; Parabola y = a(xh)^2k Author Ng Wing Shan Topic Parabola Related Topics Ellipse;



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Unit 5 Quadratic Functions Flashcards Quizlet
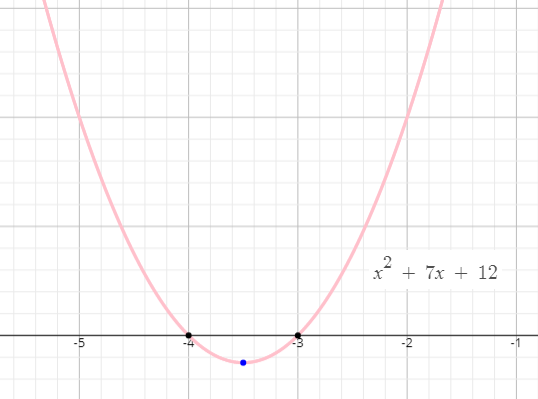
All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction ah^ {2}\left (2ax\right)hax^ {2}yk=0 a h 2 ( − 2 a x) h a x 2 − y k = 0A parabola is of the form y=(xh) ^2k It has x intercepts at (1,0) and (8,0) Determine the axis of symmetry of the curve Would somebody be able to help me with this question?Here are the steps required for Graphing Parabolas in the Form y = a (x – h) 2 k Step 1 Find the vertex Since the equation is in vertex form, the vertex will be at the point (h, k) Step 2 Find the yintercept To find the yintercept let x = 0 and solve for y Step 3 Find the xintercept (s)




Graphing Parabolas



Graph Quadratic Functions
Y 2 4y 4x = 0 se puede escribir como (Yk) 2 = 4a (x h) Sugerencia ponga todos los términos con yyy 2 juntos en un lado y todos los términos con x en el otro lado de la ecuación Completa el cuadrado de la expresión que contiene yyy 2 Encuentra a, h y k Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange anonymous assuming you mean a parabola of the form y = a (xh)^2k Then the vertex is at (h,k) The graph is that of y=x^2, but vertically scaled by a factor of a, and shifted right by h and up by k As for general quadratics, the question makes no sense 👍



Q 2 Connor Jennings




Practice 7 Fill In The Blanks The Vertex Form Of A Parabola Is Y A X H 2 K Where Is The Brainly Com
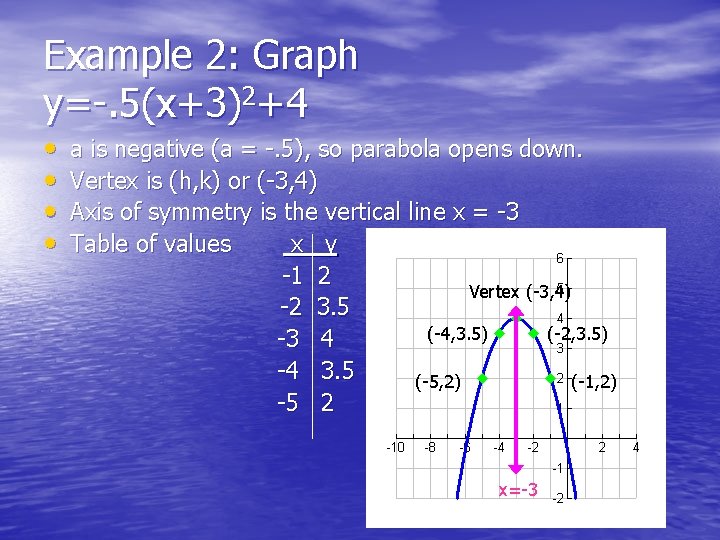
Summary Vertex form of a quadratic equation is y=a (xh) 2 k, where (h,k) is the vertex of the parabola The vertex of a parabola is the point at the top or bottom of the parabola 'h' is 6, the first coordinate in the vertex 'k' is 4, the second coordinate in the vertexLearn termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) with free interactive flashcards Choose from 63 different sets of termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) flashcards on QuizletFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience




Programmer Mathematics 22 Image And Properties Of Quadratic Function Programmer Sought



1
No headers The equation of the parabola is often given in a number of different forms One of the simplest of these forms is (x − h)2 = 4p(y − k) A parabola is defined as the locus (or collection) of points equidistant from a given point (the focus) and a given line (the directrix) Another important point is the vertex or turning point Put the equation y x² 22x 1 into the form y 2 h You will definitely start loving math once you use and see how effortless it is Transforming Quadratic Function In The Form Y A X H 2 K Graph Table Of Values Vertex Form Youtube The equation y 3x 2 12x 11 Vertex form of a parabola is y a x h 2 k How to put an equation into y=a(xh)^2kParabolas The Vertex Form of a Parabola The formula for the vertex form of a parabola is f(x) = a(x h)2 k where a = vertical stretch or shrink of the parabola and (h, k) are the (x, y) coordinates of the vertex of the parabola h = the xcoordinate and k = the ycoordinate




Quadratic Function




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id
H = _____ Relation to the Vertex The value of h is the _____ coordinate of the vertex o 2eg the vertex of y = (x 3) is _____ Role of k 2 Properties If k > 0, then the graph of y = a(x – h)2 k is



Quadratics Graphing Parabolas Sparknotes




3 Ways To Find The Inverse Of A Quadratic Function Wikihow




Quadratic Formula Calculator



How To Write An Equation For A Parabola In Vertex Form Wyzant Ask An Expert
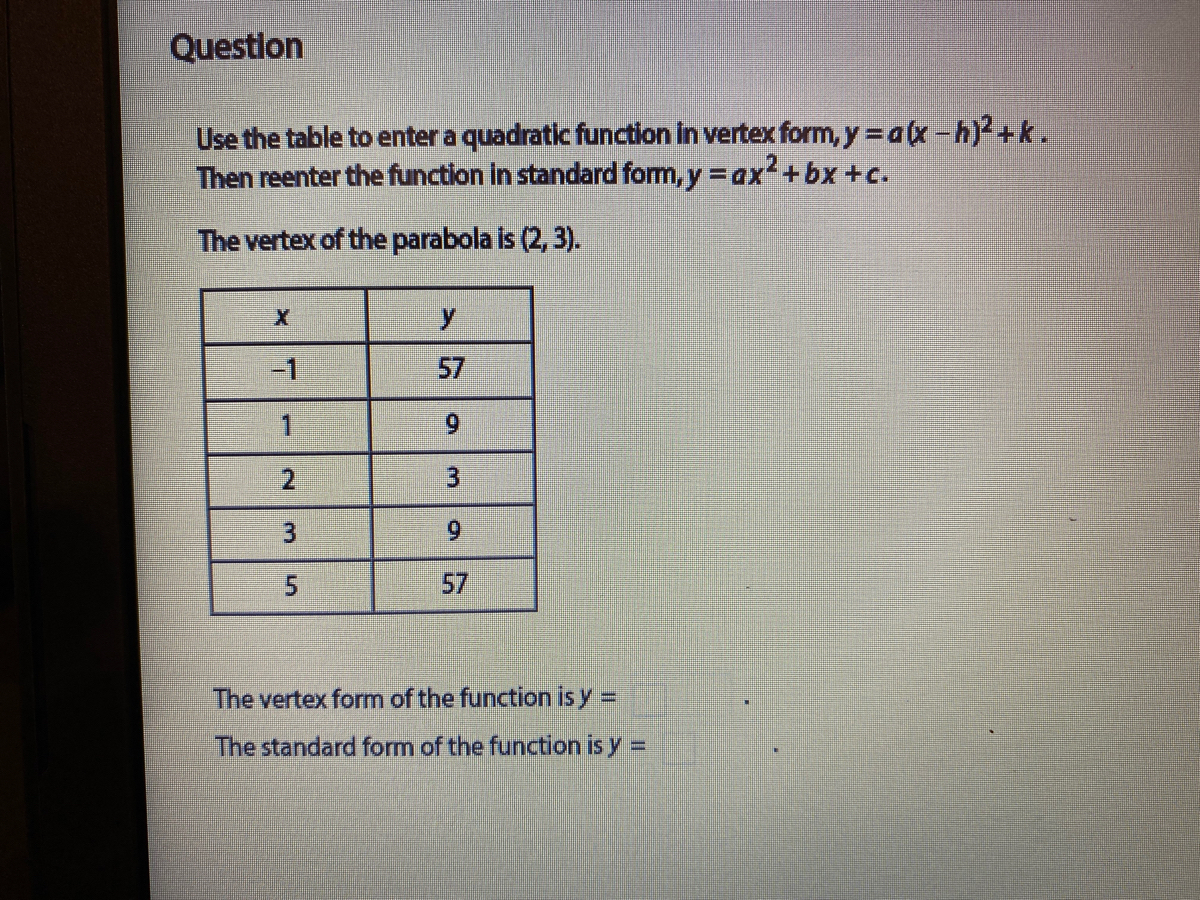



Answered Questlon Use The Table To Enter A Bartleby



Q 2 Olivia S Digital Portfolio
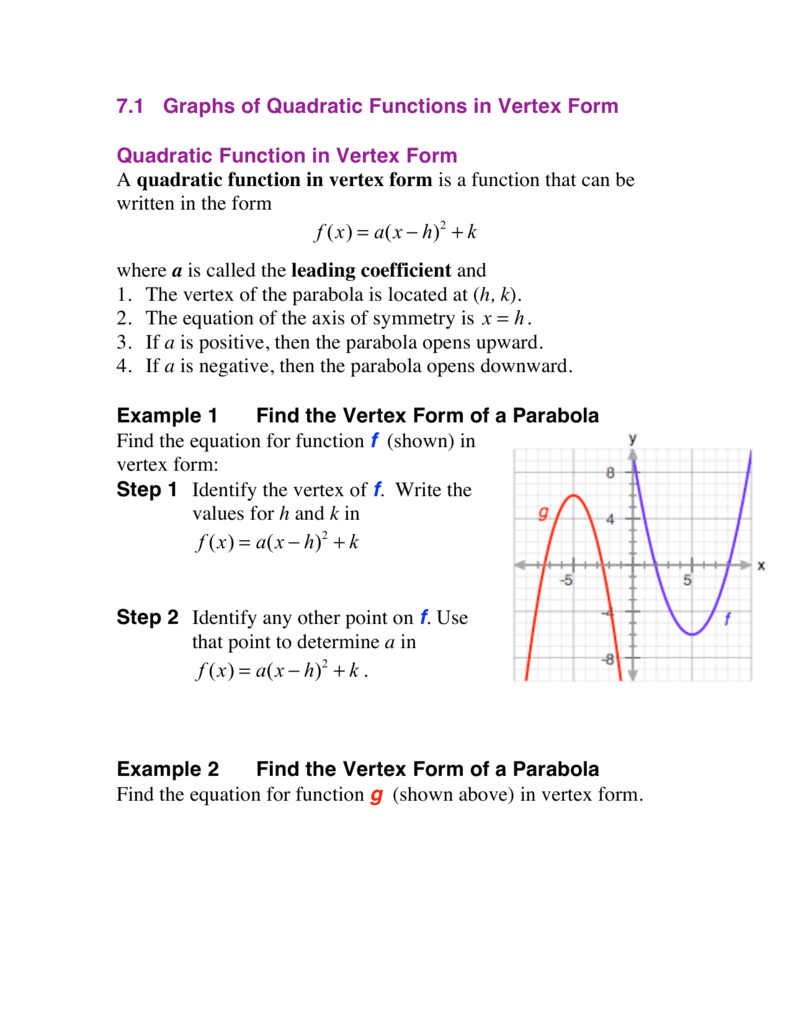



F X A X H 2 K F X A X H 2 K F X A X H 2 K



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora
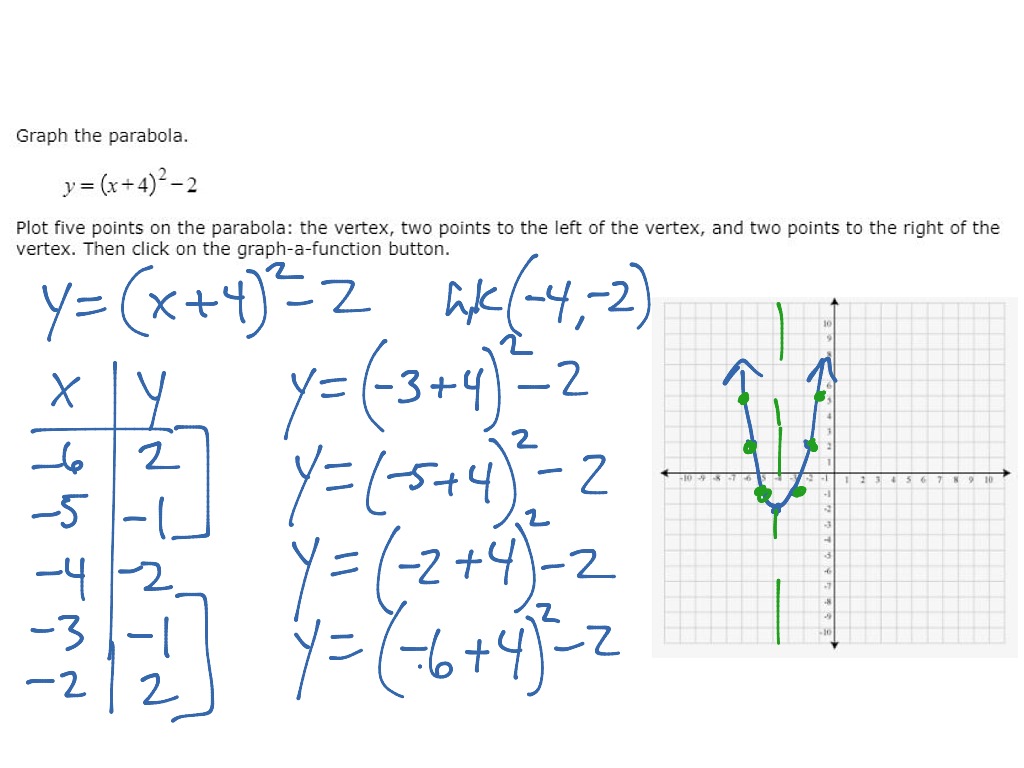



Math 1050 Graphing Parabola Y X H 2 K Math Showme




Ppt Example 1 Powerpoint Presentation Free Download Id



Math Spoken Here About Quadratics 3




Graphing Parabolas In Graphing Form Y X H 2 K Youtube



Quadratics Graphing Parabolas Sparknotes
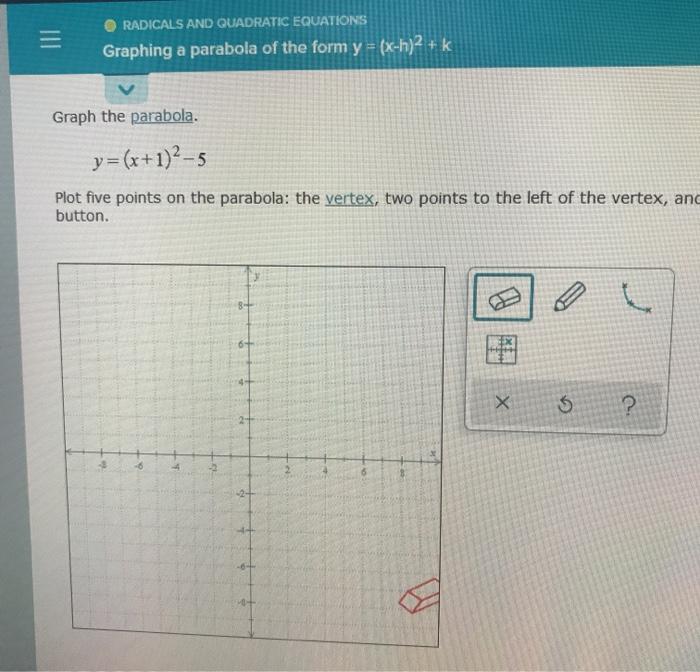



Radicals And Quadratic Equations Graphing A Parabola Chegg Com




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Finding Features Of Quadratic Functions Video Khan Academy




Standard And Vertex Form Of The Equation Of Parabola And How It Relates To A Parabola S Graph
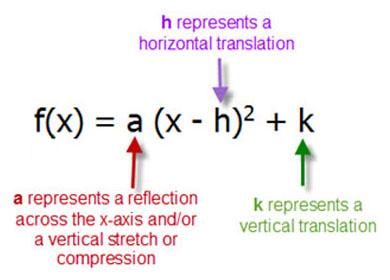



Untitled Document
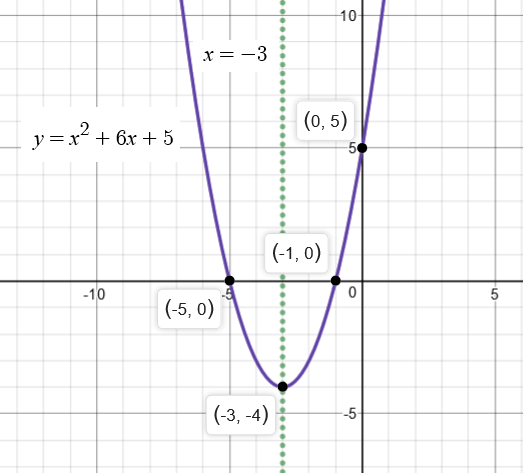



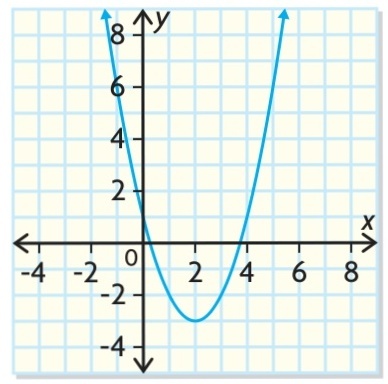
How Do Find The Vertex And Axis Of Symmetry And Intercepts For A Quadratic Equation Y X 2 6x 5 Socratic
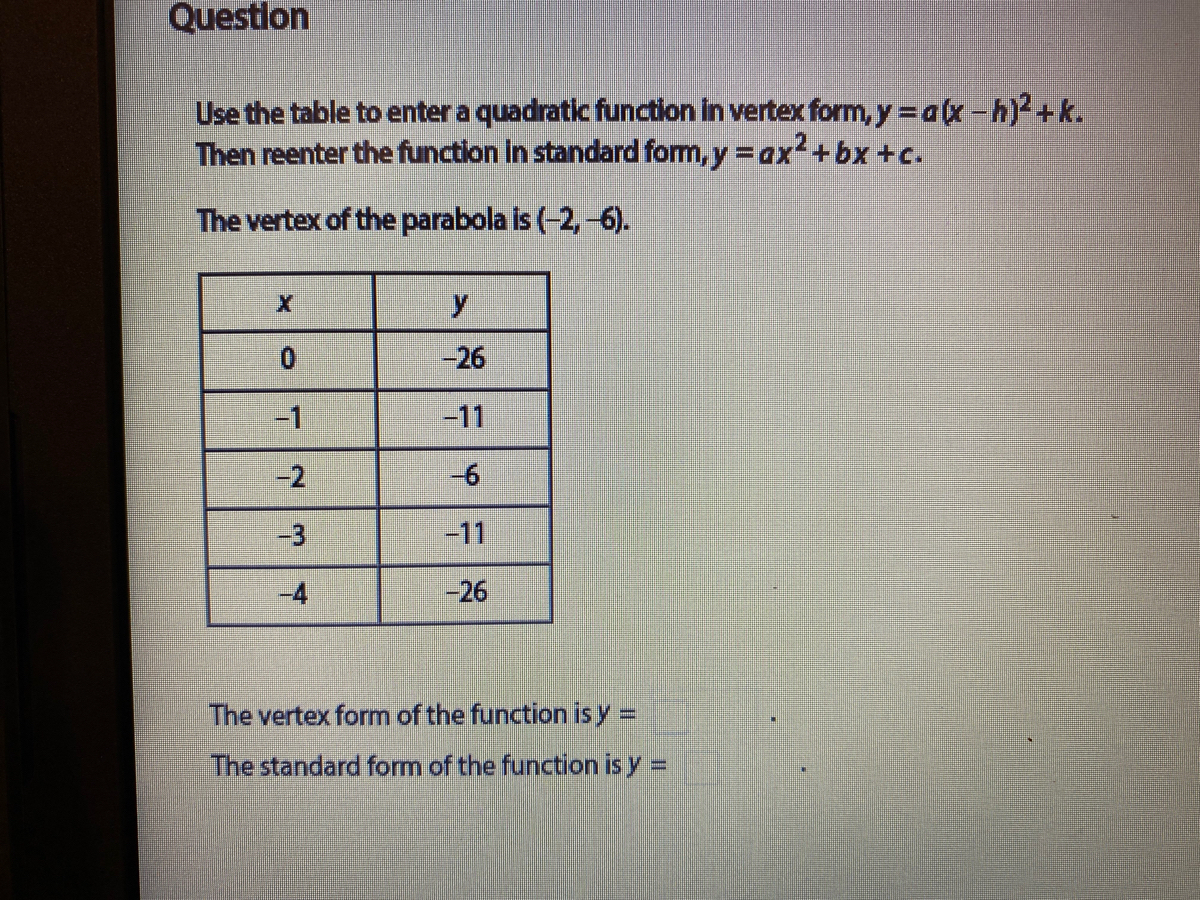



Answered Use The Table To Enter A Quadratic Bartleby



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation



5 1 Graphing Quadratic Functions P 249 Definitions



Y A X H 2 K Transformations



Completing The Square Step By Step Chilimath



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download




Explaining A And H When You Have Y A X H 2 Youtube



Lesson 4 Parabolas In This Lesson Students Will Become Familiar With The Equations And Graphs Of Parabolas The Definition Of A Parabola Will Be Learned Both Algebraically And Using The Distance Relationship Students Will Learn How To Construct A Parabola



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
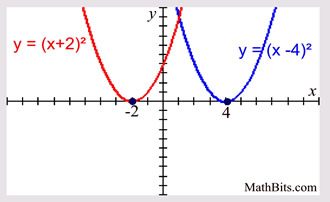



Parabola Parent Function Mathbitsnotebook A1 Ccss Math



Graphing A Parabola Of The Form Y X H 2 K Youtube




6 6 Analyzing Graphs Of Quadratic Functions



Vertex And Intercepts
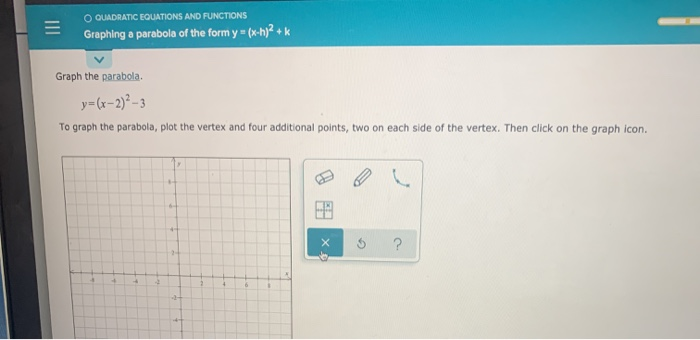



O Quadratic Equations And Functions Graphing A Chegg Com




Quadratic Functions




Consider The Parabola Graphed Below Is Of The Form Y X H 2 K Brainly Com




A X H 2 K 0 Algebra 2 Part 1
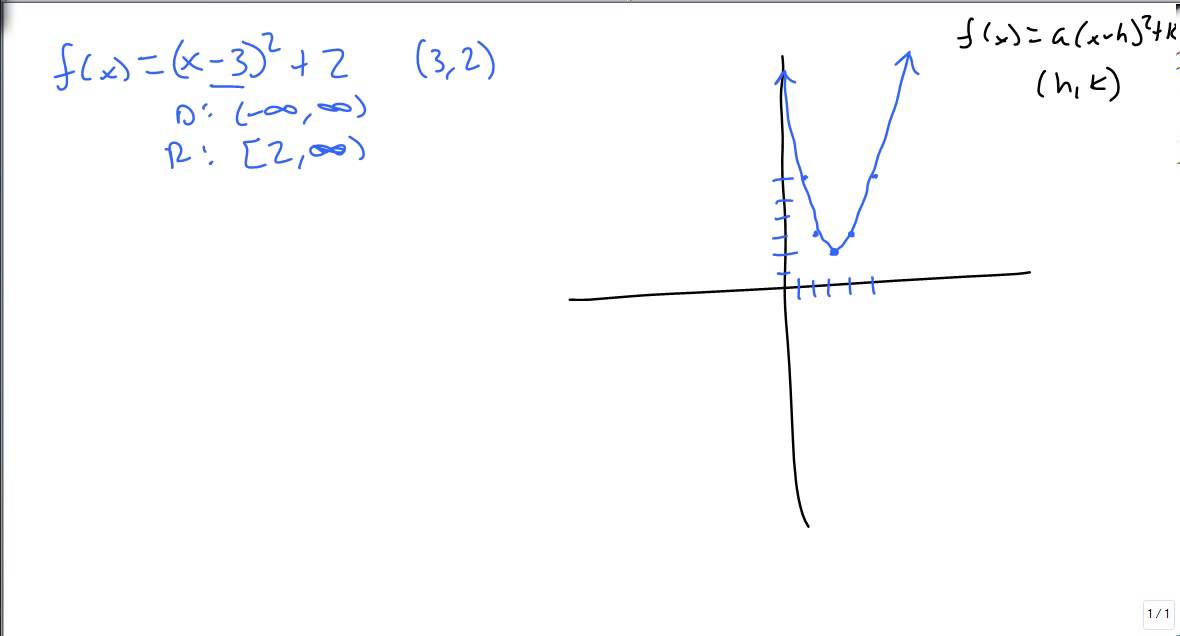



Graph By Transformations F X A X H 2 K Youtube
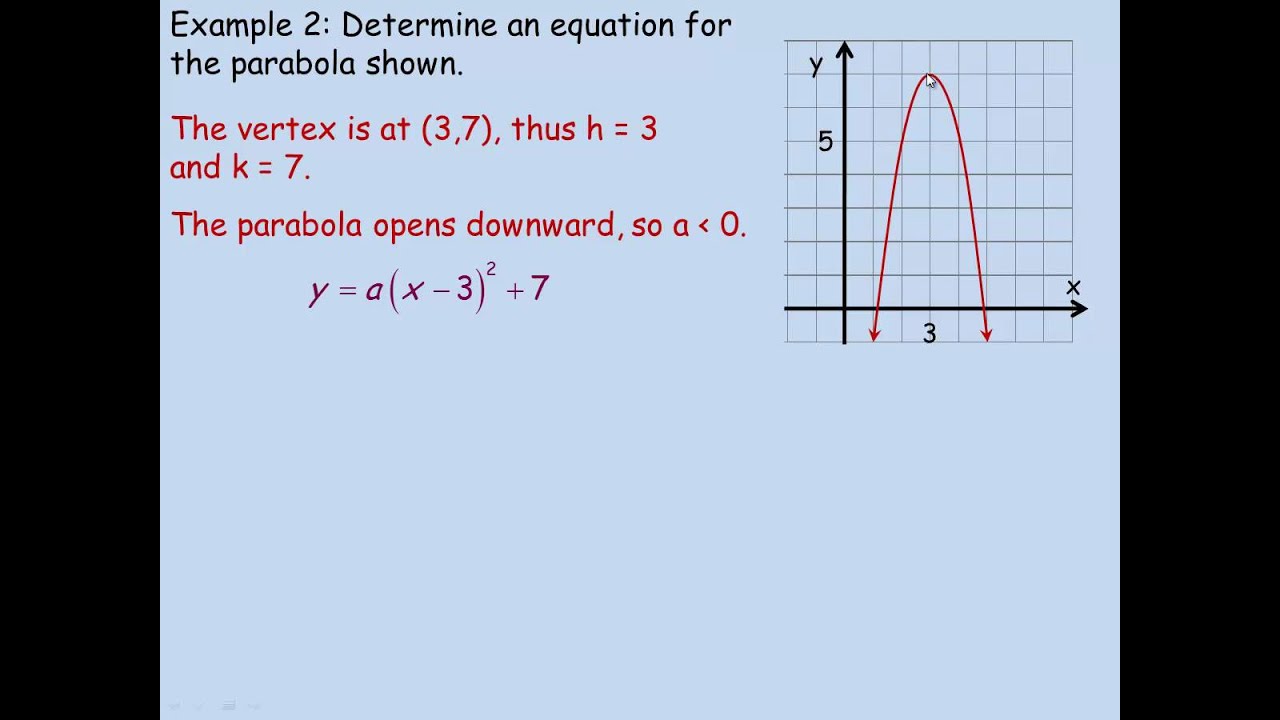



Graphing Y A X H K Youtube




How To Graph A Parabola Of The Form Y A X H 2 K Algebra Study Com
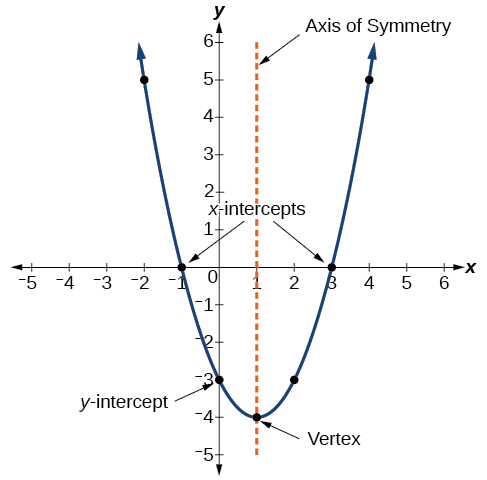



5 2 Quadratic Functions Mathematics Libretexts



Polynomial Functions Quadratic Functions Sparknotes
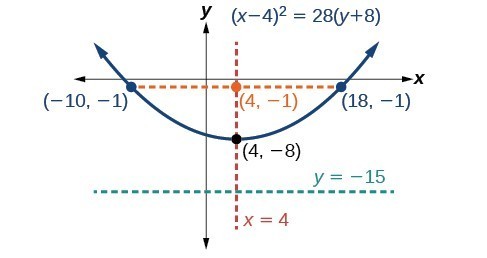



Graphing Parabolas With Vertices Not At The Origin College Algebra




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1



Illustrative Mathematics




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download



Quadratic Function Wikipedia



Graphing Quadratic Functions




Quadratic Equations Parabolas Flashcards Quizlet




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21



Http Mrsk Ca Ap 4 4vertexform Pdf
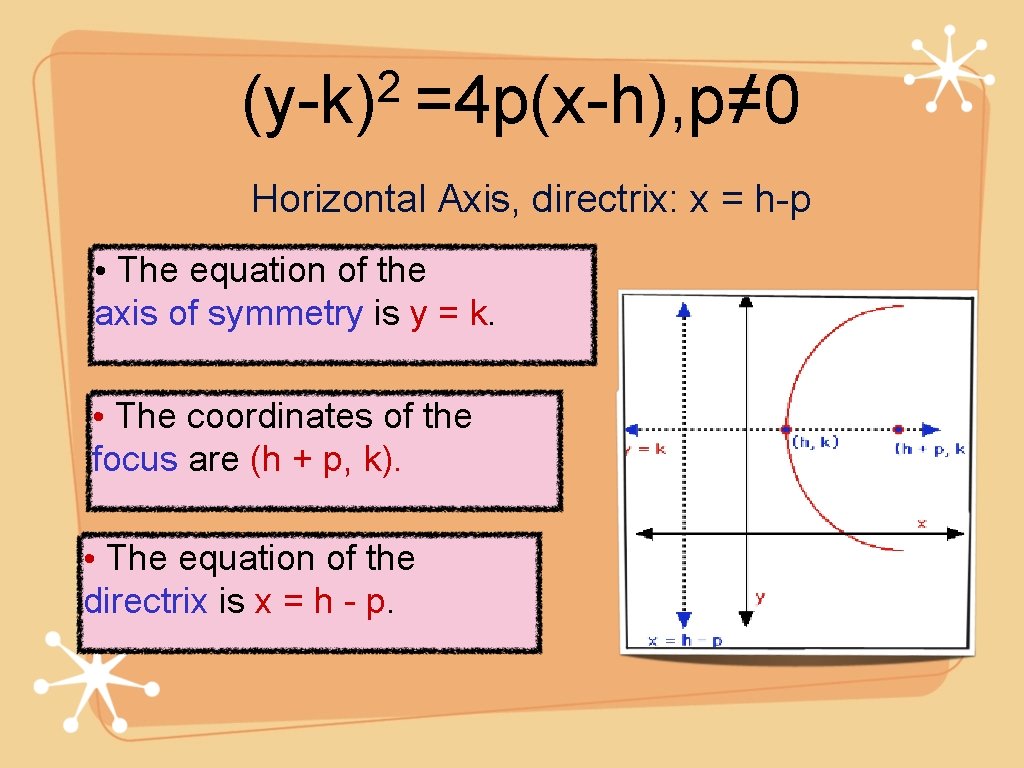



Parabola Conic Section Warmup Graph The Following Parabola
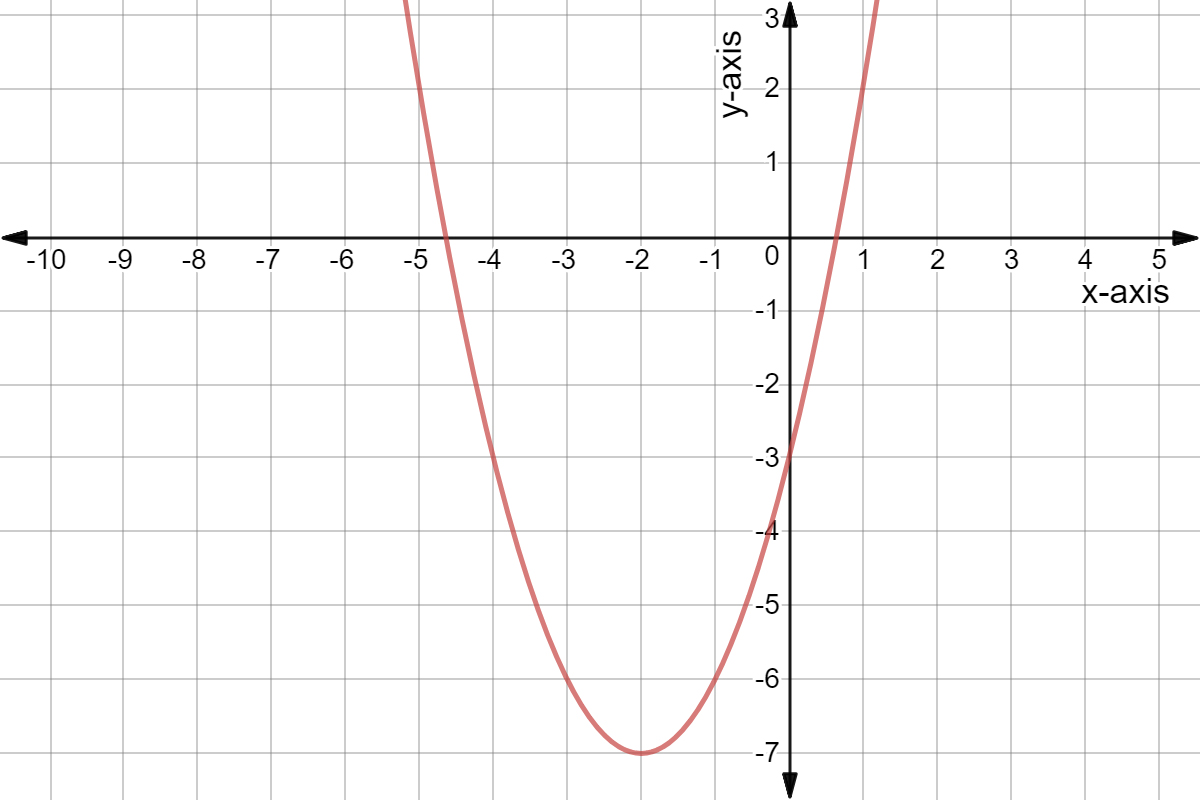



Completing The Square Vertex Form Of A Quadratic Expii




Suppose The Parabola Y K 2 4 X H With Vertex A Passe




Vertex Form Vertex Form Vertex Form Is Another




Graphing A Parabola In The Form Y X H 2 K Youtube




Warm Up Lesson Presentation Lesson Quiz Holt Mcdougal Algebra 2 Pdf Free Download




Example 35 Find Shortest Distance Of 0 C From Parabola
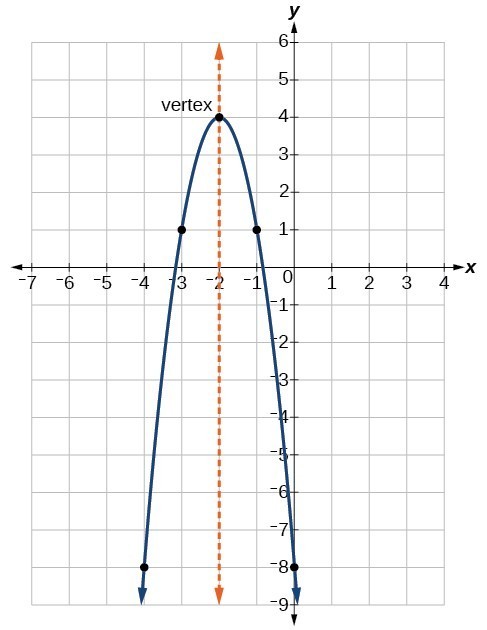



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Quadratic Functions




K That S Parabolic



1



Pslv Conic Section




Quadratic Functions
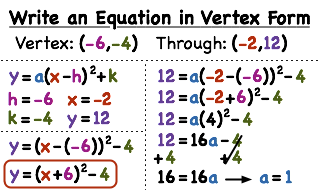



How Do You Write A Quadratic Equation In Vertex Form If You Have The Vertex And Another Point Printable Summary Virtual Nerd
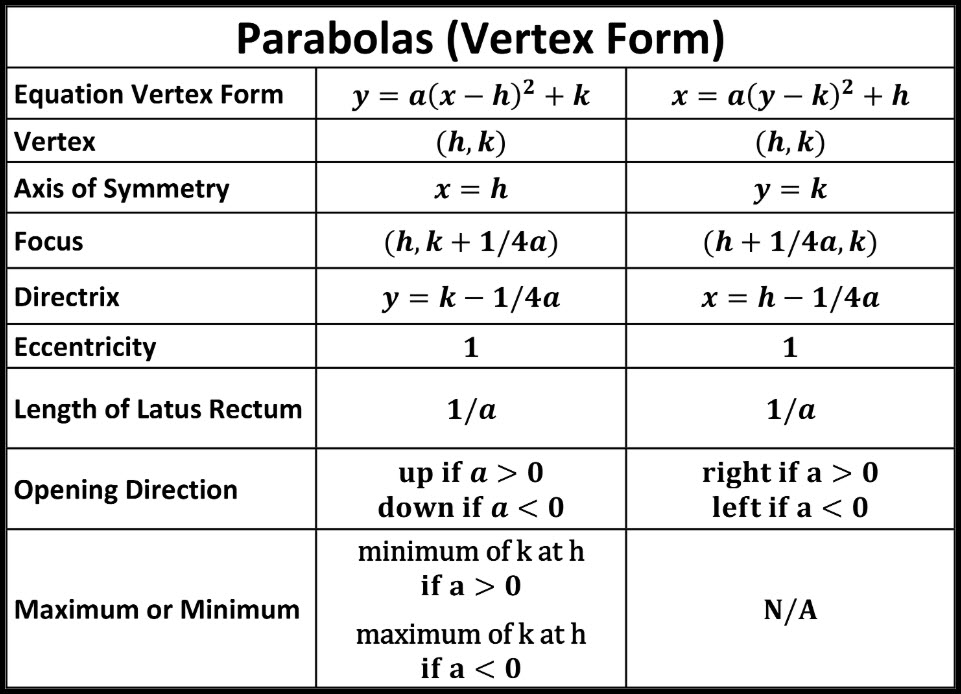



Parabolas Andymath Com




Vertex Intercept And Standard Form Read Algebra Ck 12 Foundation




How To Graph A Parabola Of The Form Y X H 2 K Algebra Study Com




X H 2 Y K 2 R 2 Examples Novocom Top




Quadratic Function Wikipedia




Completing The Square And Vertex Form Practice Quiz Quizizz
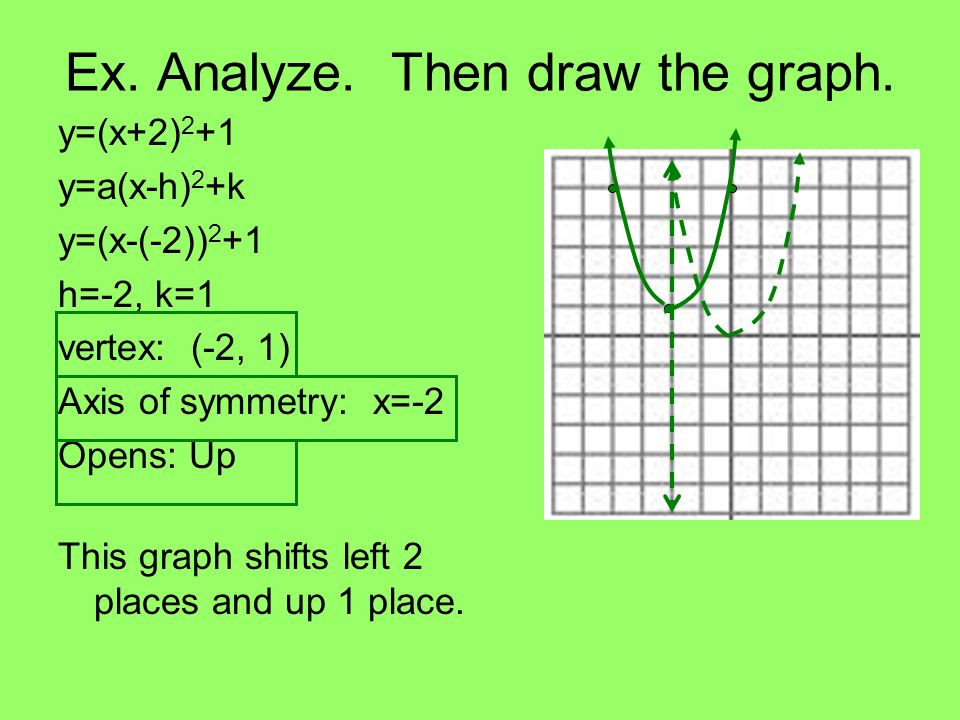



6 6 Analyzing Graphs Of Quadratic Functions Ppt Download




Shifting Parabolas Video Khan Academy




Graphing Parabolas
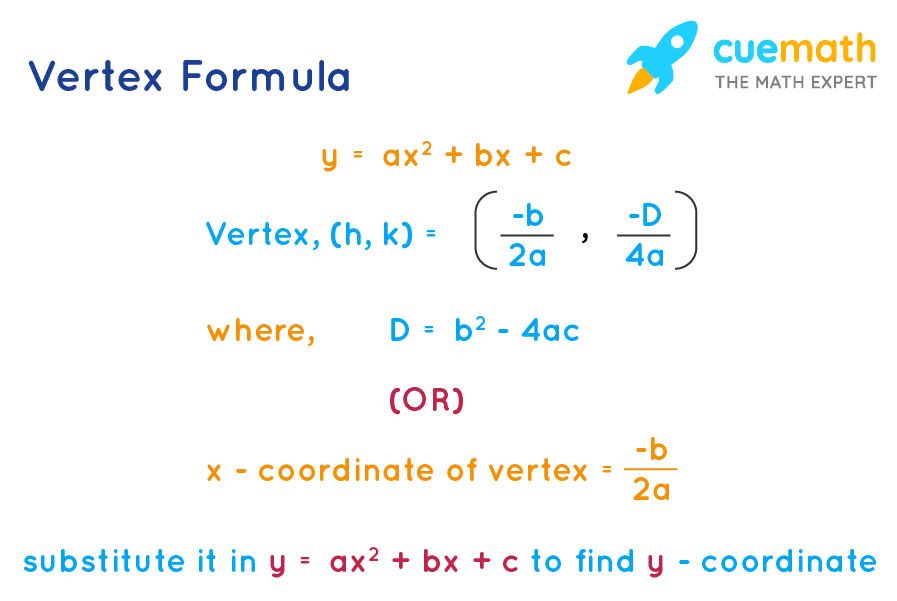



Vertex Formula What Is Vertex Formula Examples




Parabolas With Vertex At H K Ck 12 Foundation




6 6 Analyzing Graphs Of Quadratic Functions




Parabola
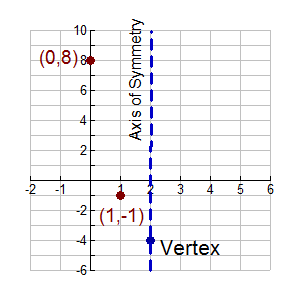



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math


